Teoria delle categorie.

Definizione di Categoria.

Non è questo il posto adatto per entrare nei dettagli della teoria delle categorie. Si tratta di una teoria affascinante, espressiva e potente. Possiamo qua solo mostrare come la definizione di categoria sia piuttosto elementare e dare dei semplici esempi.

Abbiamo detto che nella teoria delle categorie il concetto fondamentale sono le frecce.

Una freccia f dall'oggetto a all'oggetto b si indica con:

Diciamo, per semplicità, che due frecce sono consecutive se l'oggetto destinazione della prima coincide con l'oggetto sorgente della seconda.

Una categoria è una collezione di frecce tra oggetti tale che:

• Composizione: date due frecce consecutive f e g è definita la loro composizione che è una freccia g f che va dalla sorgente di f alla destinazione di g.
• Identità: per ogni oggetto a della categoria c'è una freccia i_a , detta freccia identità di a, che parte da a e finisce in a, tale che:
  per ogni freccia f che termina in a risulta i_a f = f ,per ogni freccia g che parte da a risulta g i_a = g.
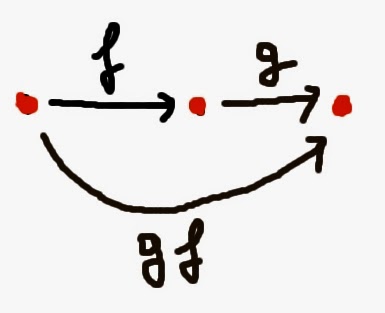
• Associatività: date tre frecce consecutive f , g , h risulta:
  h (g f) = (h g) f.

Questo è quanto è richiesto ad una collezione di frecce per essere definita una categoria.

In poche parole: le frecce si possono comporre, ogni oggetto ha una freccia che ritorna su stesso ed agisce come freccia neutra, la composizione di frecce è associativa nel senso che nella composizione hgf non importa se si compone prima h con g e poi con f, oppure se si compongono prima g con f e poi si compone con h.

La definizione può sembrare strana ma sicuramente sembrano deboli le richieste che si fanno sulle frecce e sembrano non in grado di dar luogo a una matematica espressiva e potente. Invece il fatto di incentrarsi da subito sul concetto di relazione dà alla teoria delle categorie una espressività enorme.

Un esempio immediato di categoria è dato dalla collezione degli insiemi (che giocano il ruolo di oggetti) con le funzioni (che giocano il ruolo di frecce) ma gli esempi di categorie che si possono fare sono praticamente infiniti. In generale (ma non è affatto l'unica possibilità) si ottiene una categoria considerando gli oggetti matematici con una certa struttura (esempio: spazi topologici, spazi metrici, gruppi, ...) e considerando come frecce le trasformazioni che preservano tale struttura.

Non possiamo qua spingerci oltre nella descrizione delle categorie.

Abbiamo visto come nella teoria degli insiemi molte costruzioni risultino forzate e farraginose: la coppia ordinata, il prodotto cartesiano, le relazioni, le funzioni, i numeri naturali, ...

La teoria delle categorie riesce a dare delle definizioni pulite e strutturali di tutti questi concetti e di moltissimi altri.

Quando diciamo “definizioni strutturali” intendiamo definizioni in grado di cogliere esattamente ed esclusivamente la struttura di ciò che si vuole studiare.
Così non è per esempio per la definizione dei numeri naturali data nella teoria degli insiemi. Se definiamo 0 come {}, 1 come 0 U {0}, 2 come 1 U {1}, 3 come 2 U {2} e cosi via, otteniamo qualcosa che ha le proprietà dei numeri naturali ma che ha anche molte altre proprietà casuali derivanti dalla specifica costruzione che ne stiamo dando: per esempio, secondo questa definizione, abbiamo che 1 appartiene a 3, cosa che non ha nessun significato ma è solo conseguenza della costruzione scelta.
Secondo una definizione strutturalista il numero 3 dovrebbe essere caratterizzato esclusivamente dall'occupare il terzo posto nella successione dei numeri e da nessun'altra proprietà derivante per esempio dall'insieme che si è scelto per rappresentarlo.

Un altro aspetto interessante, anche, come vedremo, per i nostri scopi, della teoria delle categorie è la sua capacità di rappresentare anche se stessa. E' qui che la teoria delle categorie prende il via verso livelli di astrazione che non esistono in nessuna altra branca della matematica. Le categorie (viste come oggetti) con le trasformazioni tra categorie (viste come frecce) formano esse stesse una categoria ... Ma qua, davvero, non possiamo spingerci oltre perché la difficoltà matematica delle astrazioni diventa esponenziale.

____________

L'aspetto che più ci interessa è questa possibilità di basare la matematica sulle frecce.

Di basare la definizione dei numeri sulle frecce. Di caratterizzare il contare con le frecce.

Ci interessa qua sottolineare l'importanza nella matematica moderna e nelle fondamenta della matematica del concetto di freccia, relazione, processo, trasformazione.

Ci interessa perché tenteremo di cogliere l'origine stessa di tali concetti nei primi processi mentali di ogni neonato.

A questo scopo dobbiamo descrivere la Teoria della Nascita di Massimo Fagioli.